Notation générale:
$$\begin{align}&\text{- Tension:}\\ &u(t)={{U_0\cos(\omega t+\phi)}}\\ &\\ &\text{-Courant:}\\ &i(t)={{I_0\cos(\omega t+\phi)}}\end{align}$$
Représentation de Fresnel:
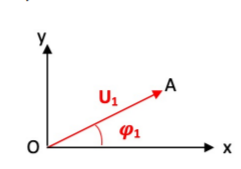
On représente la fonction par un vecteur:
- La longueur \(\iff\) Amplitude/module
- angle \(\varphi\) \(\iff\) déphasage/argument
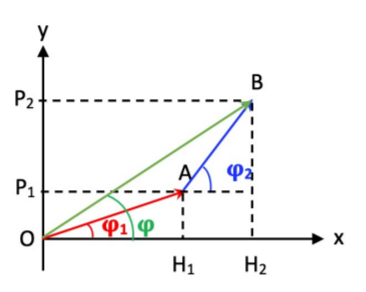
Addition en vecteurs de Fresnel:
$$OH_2=U\cos\varphi={{OH_1+H_1H_2}}={{U_1\cos\varphi_1+U_2\cos\varphi_2}}$$
$$OP_2=U\sin\varphi={{OP_1+P_1P_2}}={{U_1\sin\varphi_1+U_2\sin\varphi_2}}$$
Impédance complexe
\(Z:\text{ Impédance complexe en }{{(\Omega)}}\)
$$Z={{\frac{\underline U}{\underline I} }}={{\frac{U_0}{I_0}e^{j(\varphi_u-\varphi_i)} }}$$
$$\begin{cases}|Z|={{\frac{U_0}{I_0} }}\quad\text{donne le rapport des amplitudes d'u(t) et i(t)}\\ Arg(Z)={{\varphi_u-\varphi_i}}\quad\text{donne le déphasage d'u(t) par rapport à i(t)}\end{cases}$$
$$\begin{align}&\text{Loi d'Ohm en régime sinusoïdal}\\ &\\ &\qquad\qquad\qquad {{\underline U=Z\underline I}}\end{align}$$
$$\begin{align}& \text{Argument et module de l'impédance:}\\ \\ &\quad\quad\qquad \begin{cases}|Z|={{\frac{\underline U_0}{\underline I_0} }}\\ arg(Z)={{arctan(\frac{Im(Z)}{Re(Z)})}}\end{cases}\end{align}$$
Résistance complexe:
Courant et tension sont en phase :
$$Z=\frac{\underline U}{\underline I}=\frac{RI_0}{I_0}.\frac{e^{j\omega t} e^{j\varphi_i} }{e^{j\omega t} e^{j\varphi_i} }=R$$
\(\longrightarrow\) Représentation:
$$\begin{cases}|Z|=\frac{U_0}{I_0}={{R}}\\ arg(Z)={{0}}\end{cases}$$
Capacité complexe:
$$Z=Z_C={{\frac{1}{jC\omega} }}$$
\(\longrightarrow\) Représentation:
$$\begin{cases}|Z|=\frac{U_0}{I_0}={{\frac{1}{C\omega} }}\\ arg(Z)={{\frac{-\pi}{2} }}\end{cases}$$
Inductance complexe:
$$Z=Z_L={{jL\omega}}$$
\(\longrightarrow\) Représentation:
$$\begin{cases}|Z|=\frac{U_0}{I_0}={{L\omega}}\\ arg(Z)={{\frac\pi2}}\end{cases}$$
Admittance complexe
\(\longrightarrow\) L'admittance complexe est l'inverse de l'impédance
$$Y={{\frac{\underline I}{\underline U} }}$$
\(\longrightarrow\) Representation:
$$\begin{cases}|Y|={{\frac{1}{|Z|} }}\\ Arg(Y)={{\varphi_i-\varphi_u}}={{-Arg(Z)}}\end{cases}$$
RLC série
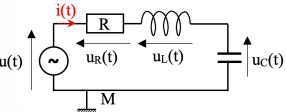
$$\begin{align}&\text{Loi des Mailles} \\ & \underline U={{\underline U_R +\underline U_L +\underline U_C}}\\ &\underline U={{(Z_R+Z_L+Z_C)\underline I}}=Z_T\underline I\\ & \text{Donc } \underline I={{\frac{\underline U}{Z_T} }}\end{align}$$
On en déduit:
$$\begin{align}&|\underline I|={{|\frac{\underline U}{Z_T}|}}\\ & \varphi_{u/i}={{Arg(Z_T)}}={{\arctan(\frac{L\omega-\frac{1}{C\omega} }{R})}}\end{align}$$
Alors:
$$i(t)={{|\underline I|cos(\omega t+\varphi_{u/i})}}$$
RLC série - Fresnel
- On choisit l'origine des phases
- On relie les vecteurs par leurs extrémités
- On trace le vecteur final en partant de l'origne jusqu'au bout du dernier vecteur
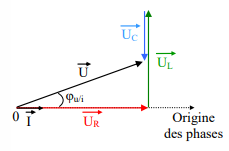
Cas spécifiques:
-impédance complexe: vecteurs orthogonnaux à l'origine des phases
-impédance réel: vecteurs colinéaires à l'origine des phases
Ponts diviseurs
Ponts diviseurs en régime permanent sinusoïdal
Thevenin - Norton
- Thevenin: un générateur de tension réel possédant une impédance interne peut-être représenté par l'association d'un générateur idéal de f.e.m. \(e_{th}(t)\) et d'une impédance complexe \(Z_{th}\) en série
- Norton: un générateur de courant réel possédant une impédance interne peut-être réprésenté par l'association d'un générateur de courant idéal de courant de court-circuit \(i_N(t)\) et d'une impédance complexe \(Z_N\) en parrallèle.
Equivalence:
$$\begin{cases}{{\underline E_{Th}=Z\underline I_N}}\\ {{Z_{Th}=Z_N}}\end{cases}$$
Puissance éléctrique